Robust estimation of reduced rank models to large spatial datasets

Abstract

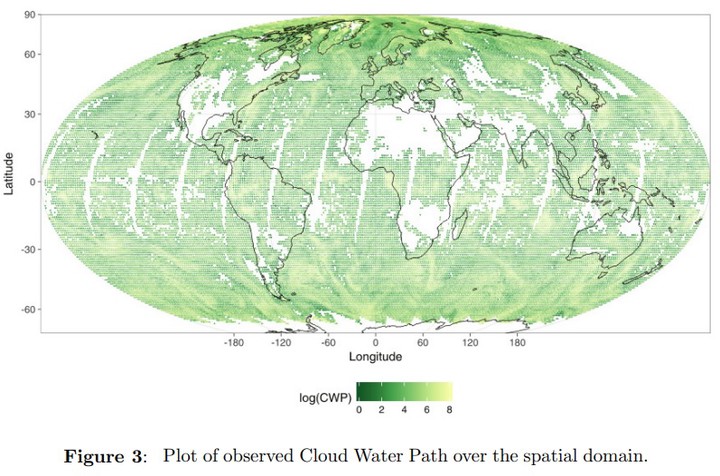
For large datasets, spatial covariances are often modeled using basis functions and covariance of a reduced dimensional latent spatial process. For skewed data, likelihood based approaches with Gaussian assumption may not lead to faithful inference. Any $L_{2}$ norm based estimation is susceptible to long tails and outliers due to contamination. Our method is based on an empirical binned covariance matrix using the median absolute deviation and minimizes $L_{1}$ norm between empirical covariance and the model covariance. The consistency of the proposed estimate is established theoretically. The improvement is demonstrated using simulated data and cloud data obtained from NASA’s Terra satellite.